Eclairement
Dans la recherche d'un réalisme toujours plus poussé, l'éclairage permet à peu de frais d'obtenir des résultats significatifs. En effet, le cerveau humain est habitué à appréhender des objets ombrés; si dans notre représentation du terrain, cela n'est plus le cas, nous nous retrouvons désorientés, sans points de repères. Le fait d'ombrer la scène permet de mieux distinguer ces détails et donne une bonne approximation des distances et des formes sans même être obligé de déplacer la camera.
Nous pouvons distinguer deux ombrages différents :
- l'éclairement direct du Soleil ;
- l'auto-ombrage.
Nous verrons dans cette partie ces deux techniques, malheureusement, faute de temps, seule la première a été implémentée dans notre programme.
Eclairement direct
Ce premier éclairement est assez simple à comprendre : pour chaque point du maillage, sa normale est calculée et une lumière (typiquement celle du Soleil) est appliquée afin de générer l'éclairement direct.
Le problème qui se pose à nous est le suivant : le LoD Bias réduit le nombre de vertices affichés et l'application du GéoMorphing modifie leur position. Leur normale n'est donc pas forcément toujours la même en fonction de la position de l'observateur. De plus, le fait d'enlever des vertices du maillage change l'affichage de manière notable : il devient impossible d'appliquer un modèle d'éclairement (OpenGL ou Cg) basé sur les vertices puisque ceux-ci peuvent être modifiés au cours du temps.
On préfère alors appliquer une texture ou l'éclairement y est pré-calculé au lancement du programme. Ce système est généralement connu sous le nom de LightMap.
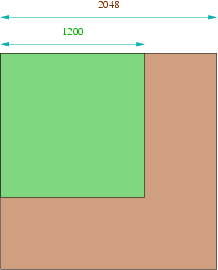
On calcule donc en fonction de la largeur et de la hauteur de la HeightMap une taille de texture optimale qu'OpenGL peut gérer : on doit donc prendre une puissance de 2 la plus petite possible permettant de contenir la carte des hauteurs en entier (tout du moins avec la version d'OpenGL que nous avons utilisée). Il est évident qu'une HeightMap dont la taille est déjà une puissance de 2 sera optimale, toutes les autres auront plus ou moins de valeurs utilisées. Par exemple, une taille légèrement plus petite que 1024 (1000*1000 par exemple) ne créera pas beaucoup d'espace inutilisé, mais 1200*1200 en créera une partie notable (puisque l'on sera obligé d'utiliser une texture de 2048*2048, comme l'indique la figure ci-dessous, qui sera entièrement passée à la carte graphique. C'est un léger désagrément qui est largement compensé par la qualité du rendu que cela apporte.
Les calculs n'étant réalisés qu'une seule fois au lancement du programme, et pouvant même être sauvegardés d'une éxécution sur l'autre, l'optimisation de cette étape de calcul n'est plus une nécessité.
Normale d'un point
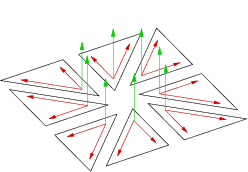
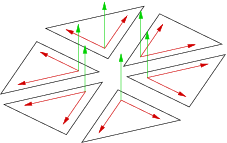
La normale en un point s'obtient en moyennant les normales des faces adjacentes à ce point. On doit donc réaliser les huit produits vectoriels de la figure ci-dessous. Dans un premier temps, nous avons souhaité réduire les calculs nécessaires; nous ne réalisons plus que les six produits vectoriels de la deuxième figure ci-dessous. Le résultat est pratiquement le même en terme de rendu visuel, tout en économisant de nombreux calculs.
Coefficient d'éclairement
Une fois que l'on possède la normale au point, il reste à trouver le coefficient d'éclairement par rapport au Soleil. Le calcul en lui-même est assez simple : en fonction de la normale, de la position du point et celle du Soleil, on souhaite obtenir un coefficient d'exposition allant de 0 (pas éclairé) à 1 (complètement éclairé). Ce coefficient correspond en fait à un produit scalaire entre le vecteur normal au point et le vecteur directeur du Soleil vers le point. Le résultat est stocké aux bonnes coordonnées de le LightMap qui est ensuite passé à OpenGL et Cg pour l'ombrage du terrain.
Auto-éclairement
L'éclairement direct présenté dans la section précédente est utile pour représenter rapidement les formes du maillage, mais n'est pas réellement correct dans le sens où l'on ne prend pas en compte le fait que le terrain peut très bien ombrer certaines parties de son propre maillage. Nous avons donc réfléchi à une manière d'augmenter le réalisme de la scène en pré-calculant aussi l'auto-éclairement directement dans la LightMap. L'idée est en fait de voir si un point est éclairé directement par le Soleil, et dans ce cas, on applique la méthode décrite plus haut, ou s'il est caché par un autre, et dans ce cas-là, son coefficient d'éclairement est mis à 0.
Pour gérer ce cas, on applique la méthode suivante pour tous les points du maillage :
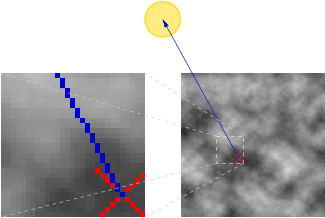
- on calcule la droite du point en cours au Soleil et on la rastérise à l'aide d'un algorithme tel que celui du point median.
- on repère si le point de cette droite est plus ou moins haut que celui
associé dans la HeightMap :
- s'il est plus bas, cela veut dire que le point que l'on est en train de tester n'est pas éclairé par le Soleil, son coefficient d'éclairement vaut donc 0 ;
- s'il est plus haut, alors on recommence en avancant d'un pas sur la droite, jusqu'à atteindre le Soleil (ou une bordure de la HeightMap) où l'on applique alors l'éclairement classique.